FUNCIONES

              

       FUNCIONES: CONCEPTOS BÁSICOS(1ª PARTE)

  

1. ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo?
      a) Una fórmula: d = m7v
      b) Una gráfica y= 0.5 x

     c) Una tabla
                 X     Y
                -2     -1
                -1    -0.5
                 0      0
                 1      0.5
                 2      1

    d) Con lenguaje natural. Ej: "la altura del árbol aumenta 5 cm por año"

 2. ¿Qué es una función? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc
   
       Una función es una relación entre un conjunto dado X y otro conjunto de elementos Y de forma que a cada elemento x le corresponde un único elemento f.

EJEMPLOS:
         

3. ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder.
 Se llama tasa de variación de la función en el intervalo, a la diferencia entre las ordenadas.
 Las funciones crecientes toman valores positivos, mientras el de las decrecientes será negativo.

                                   
 4. Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos..        
                                      
                                       
                                             
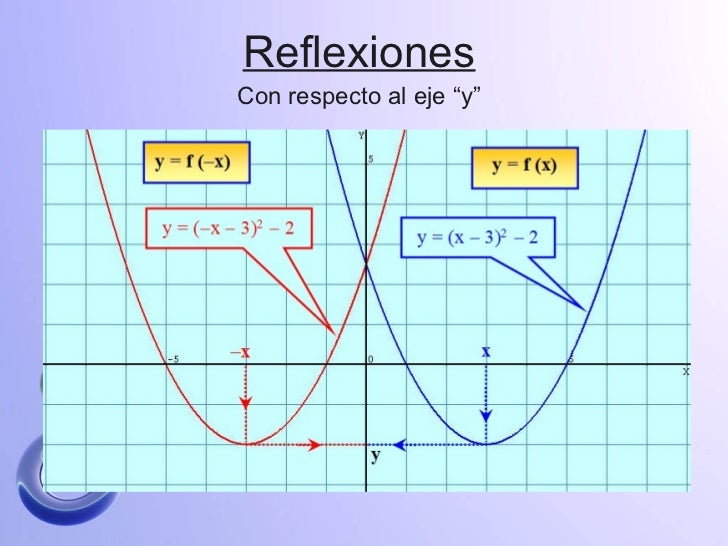
 5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría. 
                                 
                       
                                              
 6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma.
           
                 

 7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia    entre ambas?
    
               
 8. Investiga: ¿Cuál es el origen del término función?
  La palabra función viene del latín functio, ‘Ejecución, ejercicio de alguna facultad,   cumplimiento de un deber’, y además del verbo fungi, ‘cumplir, desempeñar una función,      satisfacer, emplear,...’

9.Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas.
  a) Función lineal creciente
             
b) Función lineal constante
             
c) Función lineal decreciente
                
d) Rectas paralelas
            
e) Función cuadrática cóncava
             
f) Función cuadrática convexa